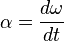|
La
cinemática estudia los movimientos de los cuerpos independientemente de las
causas que lo producen. En este capítulo, estudiaremos los movimientos
rectilíneos y curvilíneos, y circulares.
En el
caso del movimiento rectilíneo, se simularán dos prácticas que realizan los
estudiantes en el laboratorio, que consiste en un móvil que desliza por un
carril sin apenas rozamiento. En la primera práctica simulada, se determinará
la velocidad constante de un móvil, en la segunda, se determinará la
aceleración de un móvil en movimiento uniformemente acelerado.
Ambas
prácticas, se prestan especialmente para representar en una gráfica los datos
obtenidos y aplicar el procedimiento denominado regresión lineal, trazando la
recta que mejor ajusta a los resultados experimentales. Se completa aquí el
capítulo primero, en la parte correspondiente a las medidas.
MOVIMIENTO RECTILÍNEO UNIFORME
Un movimiento es rectilíneo cuando un
objeto describe una trayectoria recta, y es uniforme cuando su velocidad es constante
en el tiempo, dado que su aceleración es nula. Es indicado mediante
el acrónimo MRU, aunque en algunos países es MRC, por movimiento
rectilíneo constante.
El MRU se caracteriza por:
·
Movimiento que se realiza sobre una línea recta.
·
Velocidad constante; implica magnitud y dirección constantes.
·
La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
·
Aceleración nula.
La distancia recorrida se calcula
multiplicando la magnitud de la velocidad por
el tiempo transcurrido. Esta relación también es aplicable si la trayectoria no
es rectilínea, con tal que la rapidez o
módulo de la velocidad sea constante. Por lo tanto el movimiento puede
considerarse en dos sentidos; una velocidad negativa representa un movimiento
en dirección contraria al sentido que convencionalmente hayamos adoptado como
positivo.
De acuerdo con la Primera Ley de
Newton, toda partícula permanece en reposo o en movimiento
rectilíneo uniforme cuando no hay una fuerza externa que actúe sobre el cuerpo,
dado que las fuerzas actuales están en equilibrio, por lo cual su estado es de
reposo o de movimiento rectilíneo uniforme. Esta es una situación ideal, ya que
siempre existen fuerzas que tienden a alterar el movimiento de las partículas,
por lo que en el movimiento rectilíneo uniforme (MRU) es difícil encontrar la
fuerza amplificada.
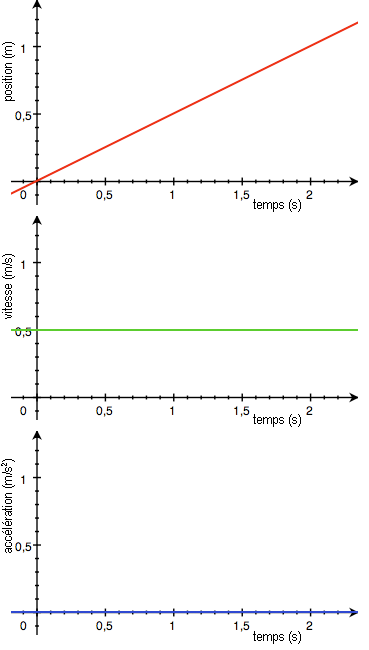
Representación gráfica del movimiento
Al
representar gráficamente en un sistema de coordenadas cartesianas, la velocidad
en función del tiempo se obtiene una recta paralela al eje
de abscisas (tiempo). Además, el
área bajo la recta producida
representa la distancia recorrida.
La
representación gráfica de la distancia recorrida en función del tiempo da lugar
a una recta cuya pendiente se corresponde con la velocidad.
Ecuaciones del movimiento
Sabemos que la velocidad
 es constante; esto significa que no existe aceleración. es constante; esto significa que no existe aceleración.
La posición
 en cualquier instante en cualquier instante  viene dada por viene dada por
Para una posición inicial
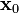 y un tiempo inicial y un tiempo inicial 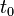 , ambos distintos de cero, la posición para cualquier tiempo está dada por , ambos distintos de cero, la posición para cualquier tiempo está dada porMOVIMIENTO RECTILÍNEO UNIFORMEMENTE ACELERADO(MRUA)
El movimiento rectilíneo uniformemente acelerado (MRUA) es el movimiento de una partícula o cuerpo por una línea recta con una aceleración constante. Es decir:
En este ejemplo vemos como el objeto va aumentando su velocidad uniformemente conforme va pasando el tiempo y avanza por su trayectoria.
Posición
La posición de la partícula en el tiempo t aumenta (o disminuye) exponencialmente en función de la aceleración.
Velocidad
La velocidad del cuerpo o partícula cambia linealmente en el transcurso del tiempo. Es decir, para un mismo incremento de tiempo se produce un mismo incremento de velocidad por la constancia de la aceleración.
En el siguiente gráfico podemos observar como el incremento de la velocidad es igual cuando transcurre el mismo tiempo por su linealidad.
Aceleración
El cuerpo que lleva un movimiento MRUA mantiene una aceleración constante:
Ejemplo
Un caso particular de movimiento rectilíneo uniformemente acelerado (MRUA) es la caída libre de un cuerpo o su lanzamiento vertical con una velocidad v0.
CAÍDA LIBRE
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como un disparo vertical; o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de un cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
FORMULAS |
TIRO VERTICAL
El tiro vertical es un movimiento sujeto a la aceleración gravitacional, solo que ahora es la aceleración la que se opone al movimiento inicial del objeto. El tiro vertical comprende subida y bajada de los cuerpos u objetos.
CARACTERISTICAS:
- Nunca la velocidad inicial es cero.
- Cuando el objeto alcance su altura máxima su velocidad en este punto es cero, mientras el objeto está de subida el signo de la velocidad es positivo y la velocidad es cero en su altura máxima, cuando comienza el descenso el signo de la velocidad es negativo.
- La velocidad de subida es igual a la de bajada pero el signo de la velocidad al descender es negativo.
Las formulas que se aplican son las mismas que en el M.R.U.A.

MOVIMIENTO DE PROYECTILES
Imagina que se lanza un objeto con velocidad Vo que forma con la horizontal un Angulo x. La velocidad inicial tiene dos componentes:
Vox = Vo . cos
Voy = Vo . sen
 .
.
El movimiento de proyectil es un movimiento combinado: el proyectil tiene movimiento vertical y, además, se desplaza horizontalmente, recorriendo distancias iguales en tiempos iguales .
QUE ES UN PROYECTIL?
El movimiento de un proyectil es un ejemplo clásico del movimiento en dos dimensiones con aceleración constante. Un proyectil es cualquier cuerpo que se lanza o proyecta por medio de alguna fuerza y continúa en movimiento por inercia propia. Un proyectil es un objeto sobre el cual la única fuerza que actúa es la aceleración de la gravedad. La gravedad actúa para influenciar el movimiento vertical del proyectil. El movimiento horizontal del proyectil es el resultado de la tendencia de cualquier objeto a permanecer en movimiento a velocidad
El término proyectil se aplica por ejemplo a una bala disparada por un arma de fuego, a un cohete después de consumir su combustible, a un objeto lanzado desde un avión o en muchas actividades deportivas (golf, tenis, fútbol, béisbol, atletismo etc.). L os fuegos artificiales y las fuentes del agua son ejemplos del movimiento de proyectiles . El camino seguido por un proyectil se denomina trayectoria . El estudio del movimiento de proyectiles es complejo debido a la influencia de la resistencia del aire, la rotación de la Tierra, variación en la aceleración de la gravedad.

Análisis del movimiento de proyectiles
Se examina sólo trayectorias suficientemente cortas para que la fuerza gravitacional se pueda considerar constante en magnitud y dirección. También hay que analizar no tener en cuenta los efectos de la resistencia del aire; Estas hipótesis simplificadas constituyen la base de un modelo del problema físico. Como, en este caso idealizado, la única fuerza que actúa sobre el proyectil es su peso considerado constante en magnitud y dirección, es mejor referir el movimiento a un sistema de ejes coordenadas rectangulares. Se toma el eje x horizontal y el eje y verticalmente hacia arriba.
La componente x de la fuerza que actúa sobre el proyectil es nula y la componente y es el peso del proyectil – mg. Esto es, la componente horizontal de la aceleración es nula, y la componente vertical hacia abajo, es igual a la de un cuerpo que cae libremente. Puesto que la aceleración nula significa velocidad constante, el movimiento puede definirse como una combinación de movimiento horizontal con velocidad constante y movimiento vertical con aceleración constante.
Vox = Vo . cos
Voy = Vo . sen
El movimiento de proyectil es un movimiento combinado: el proyectil tiene movimiento vertical y, además, se desplaza horizontalmente, recorriendo distancias iguales en tiempos iguales .
QUE ES UN PROYECTIL?
El movimiento de un proyectil es un ejemplo clásico del movimiento en dos dimensiones con aceleración constante. Un proyectil es cualquier cuerpo que se lanza o proyecta por medio de alguna fuerza y continúa en movimiento por inercia propia. Un proyectil es un objeto sobre el cual la única fuerza que actúa es la aceleración de la gravedad. La gravedad actúa para influenciar el movimiento vertical del proyectil. El movimiento horizontal del proyectil es el resultado de la tendencia de cualquier objeto a permanecer en movimiento a velocidad
El término proyectil se aplica por ejemplo a una bala disparada por un arma de fuego, a un cohete después de consumir su combustible, a un objeto lanzado desde un avión o en muchas actividades deportivas (golf, tenis, fútbol, béisbol, atletismo etc.). L os fuegos artificiales y las fuentes del agua son ejemplos del movimiento de proyectiles . El camino seguido por un proyectil se denomina trayectoria . El estudio del movimiento de proyectiles es complejo debido a la influencia de la resistencia del aire, la rotación de la Tierra, variación en la aceleración de la gravedad.
Análisis del movimiento de proyectiles
Se examina sólo trayectorias suficientemente cortas para que la fuerza gravitacional se pueda considerar constante en magnitud y dirección. También hay que analizar no tener en cuenta los efectos de la resistencia del aire; Estas hipótesis simplificadas constituyen la base de un modelo del problema físico. Como, en este caso idealizado, la única fuerza que actúa sobre el proyectil es su peso considerado constante en magnitud y dirección, es mejor referir el movimiento a un sistema de ejes coordenadas rectangulares. Se toma el eje x horizontal y el eje y verticalmente hacia arriba.
La componente x de la fuerza que actúa sobre el proyectil es nula y la componente y es el peso del proyectil – mg. Esto es, la componente horizontal de la aceleración es nula, y la componente vertical hacia abajo, es igual a la de un cuerpo que cae libremente. Puesto que la aceleración nula significa velocidad constante, el movimiento puede definirse como una combinación de movimiento horizontal con velocidad constante y movimiento vertical con aceleración constante.
Movimiento circular
El movimiento circular (también
llamado movimiento circunferencial) es el que se basa en un eje de
giro y radio constante, por lo cual la trayectoria es una circunferencia. Si además, la velocidad de
giro es constante (giro ondulatorio), se produce el movimiento
circular uniforme, que es un caso particular de movimiento circular,
con radio y centro fijos y velocidad angular constante.
En el movimiento
circular hay que tener en cuenta algunos conceptos básicos para la
descripción cinemática y dinámica del mismo:
·
Eje de giro:
es la línea recta alrededor de la cual se realiza la rotación, este eje puede
permanecer fijo o variar con el tiempo pero para cada instante concreto es el
eje de la rotación (considerando en este caso una variación infinitesimal o
diferencial de tiempo). El eje de giro define un punto llamado centro
de giro de la trayectoria descrita (O).
·
Arco: partiendo
de un centro fijo o eje de giro fijo, es el espacio recorrido en la trayectoria
circular o arco de radio unitario con el que se mide el desplazamiento angular.
Su unidad es el radián (espacio
recorrido dividido entre el radio de la trayectoria seguida, división de
longitud entre longitud, adimensional por tanto).
·
Velocidad angular: es la variación del
desplazamiento angular por unidad de tiempo (omega minúscula, )
)
 )
)
·
Aceleración angular:
es la variación de la velocidad angular por unidad de tiempo (alfa minúscula,  ).
).
 ).
).
En dinámica de
los movimientos curvilíneos, circulares y/o giratorios se tienen en cuenta
además las siguientes magnitudes:
·
Momento angular (L): es la magnitud que
en el movimiento rectilíneo equivale al momento lineal o cantidad de movimiento
pero aplicada al movimiento curvilíneo, circular y/o giratorio (producto
vectorial de la cantidad de movimiento por el vector posición, desde el centro
de giro al punto donde se encuentra la masa puntual).
·
Momento de inercia (I):
es una cualidad de los cuerpos que depende de su forma y de la distribución de
su masa y que resulta de multiplicar una porción concreta de la masa por la
distancia que la separa al eje de giro.
·
Momento de fuerza (M): o par motor es la
fuerza aplicada por la distancia al eje de giro (es el equivalente a la fuerza
agente del movimiento que cambia el estado de un movimiento rectilíneo).
Velocidad angular y velocidad tangencial
- Velocidad angular es la variación del arco angular o posición angular respecto al tiempo. Es representada con la letra
 (omega minúscula) y viene definida como:
(omega minúscula) y viene definida como:
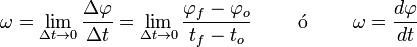
Siendo la segunda ecuación la de la velocidad angular instantánea (derivada de la posición angular con respecto del tiempo).
- Velocidad tangencial de la partícula es la velocidad del objeto en un instante de tiempo (magnitud vectorial con módulo, dirección y sentido determinados en ese instante estudiado). Puede calcularse a partir de la velocidad angular. Si
 es el módulo la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que:
es el módulo la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que:
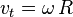
 (omega minúscula) y viene definida como:
(omega minúscula) y viene definida como: es el módulo la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que:
es el módulo la velocidad tangencial a lo largo de la trayectoria circular de radio R, se tiene que: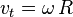
Aceleración angular y tangencial
La aceleración angular es la variación de la velocidad angular por unidad de tiempo y se representa con la letra:  y se la calcula:
y se la calcula:
 y se la calcula:
y se la calcula:
Si at es la aceleración tangencial, a lo largo de la circunferencia de radio R, se tiene que:
Período y frecuencia
El período indica el tiempo que tarda un móvil en dar una vuelta a la circunferencia que recorre. Se define como:
La frecuencia es la inversa del periodo, es decir, las vueltas que da un móvil por unidad de tiempo. Se mide en hercios o s-1
 .
.